The Power of Schemas
This article is Part 2 of our three-part series, AI Needs Data Discipline. In Part 1, we explored schema-on-write vs. schema-on-read and how hybrid systems emerged. Here we turn to the mathematical foundations: how relational models, entity-relationship diagrams, and schemas express relationships more powerfully than metadata alone. In Part 3, we’ll examine how these foundations must evolve for modern AI-driven challenges.
The structured data approaches, particularly the schema-on-write philosophy we discussed in our previous post, weren't born out of a desire for corporate rigidity. Their origins are deeply rooted in mathematical rigor and the quest for expressive, provable methods of managing data.
The Mathematical Bedrock of Order
The intellectual lineage of structured data traces back to 19th-century mathematicians like De Morgan, Boole, and Cantor, who formalized logic and set theory. These mathematical tools laid the groundwork for the relational data model, which was formalized by Edgar F. Codd in the late 1960s and early 1970s. Codd’s model was a direct application of Set Theory and predicate logic to data management. Designing schemas was no longer like intuitively nailing boards together; it's akin to using precise engineering principles—physics, material science, geometry—to design a bridge, ensuring its stability and longevity through provable calculations.
Before the relational model, data systems like hierarchical and network models often embedded relationships directly within data records. While functional, they could be complex to query and lacked a strong theoretical basis for data independence and integrity. Codd’s innovation was to represent data as mathematical "relations" (visualized as tables), where relationships are expressed through shared values (keys) rather than physical pointers. This offered a clear, declarative way to define data structures (schemas), enforce constraints, and query data using logical operations. The goal was precision and consistency, not arbitrary inflexibility.
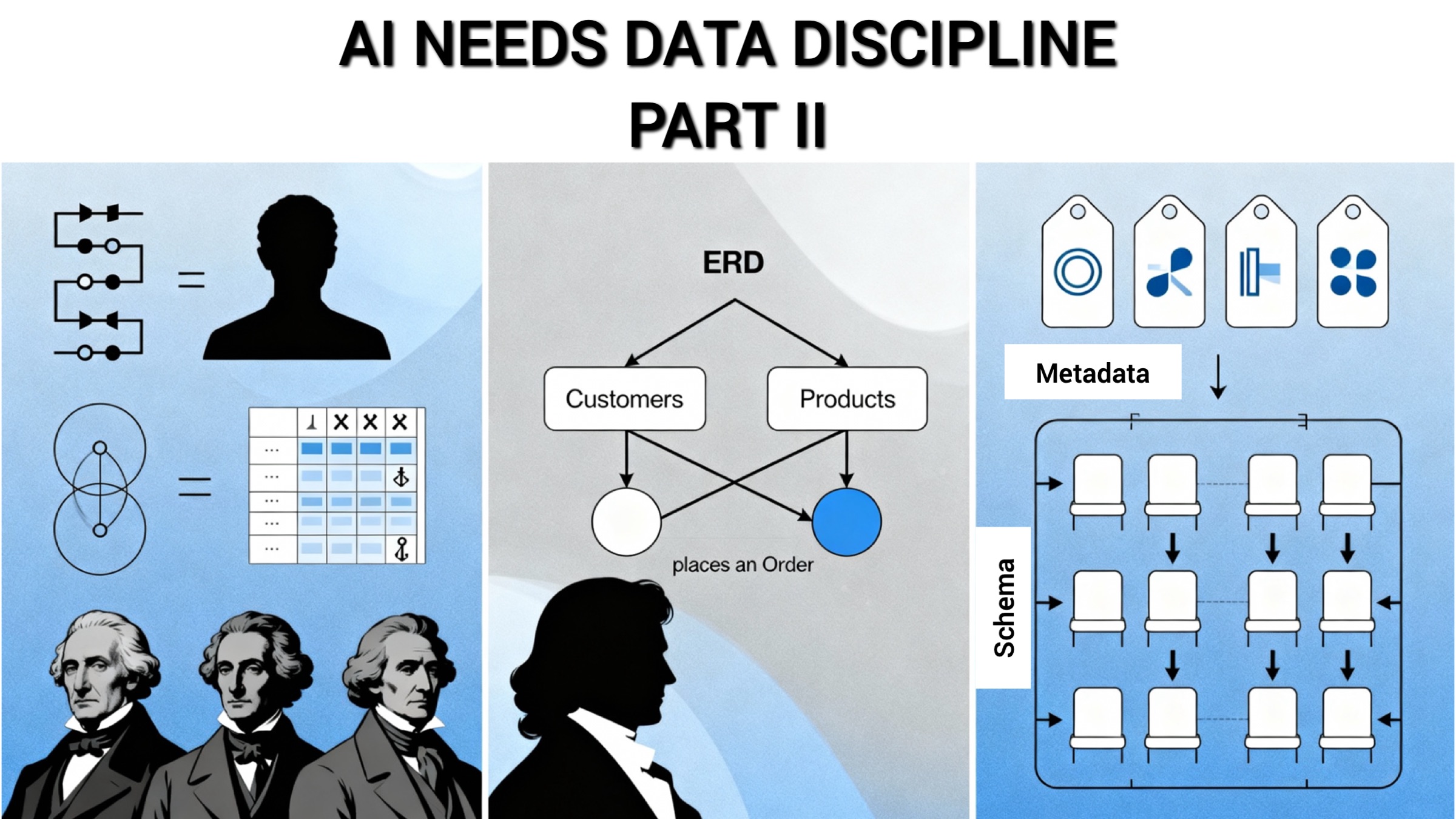
Building on this, Peter Chen introduced the Entity-Relationship Model (ERM) in 1976. While Codd provided the mathematical underpinnings, Chen’s ERM offered a more intuitive, conceptual way to design databases. ERM focuses on identifying "entities" (e.g., 'Customers,' 'Products') and the "relationships" between them (e.g., a 'Customer' places an 'Order'). Entity-Relationship Diagrams (ERDs) became a standard graphical tool to visualize these, acting as a blueprint before database implementation. It's important to note that the relational model and ERM are the foundational principles, while SQL (Structured Query Language) is the common language used to implement these principles in databases.
Metadata Implies Relationships whereas Schemas Express and Enforce Them
So, how do we truly "understand" the relationships within data? One could argue this understanding is crystallized through the act of constructing a schema.
Metadata, or "data about data," is incredibly valuable. It provides context, aids discoverability, and tracks provenance. For instance, metadata is like tagging a passenger with her destination and her luggage with her name. This provides useful context for her journey.
A formal schema, on the other hand, expresses and enforces these relationships as an intrinsic, verifiable part of the data system that supports an enterprise. Continuing our travel analogy, the schema is what guarantees the passenger her assigned seat on the correct flight and ensures her luggage makes the correct flight transfers. Foreign key constraints within a schema don't just describe a link; they actively prevent operations that would violate that link, ensuring referential integrity is maintained by the database itself. This active enforcement provides a far stronger guarantee of consistency than descriptive metadata alone.
While the relational model provides a powerful foundation, how does it fare against the scale and complexity of modern data, especially with the rise of AI? In Part 3 of AI Needs Data Discipline, "AI and the Evolution of Relational Schemas," we'll explore these challenges and why the need for structure persists.
Related posts
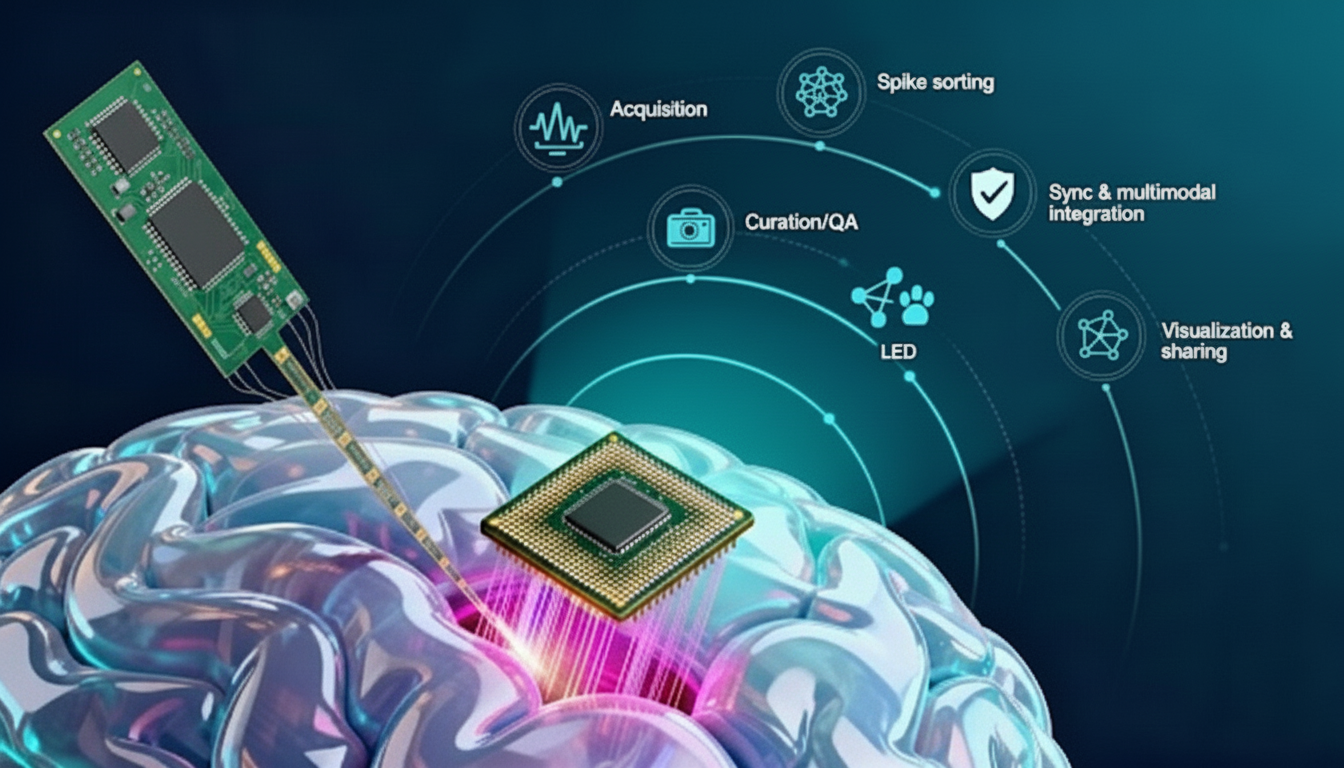
Neuropixels, Plainly Explained
AI and the Evolution of Relational Schemas
Insight Entrepreneurship – A New Vision for Science
Updates Delivered *Straight to Your Inbox*
Join the mailing list for industry insights, company news, and product updates delivered monthly.

.svg)